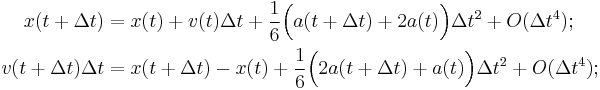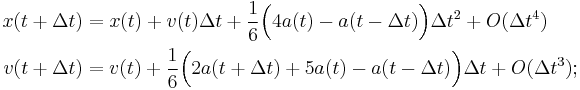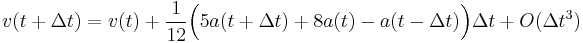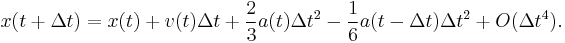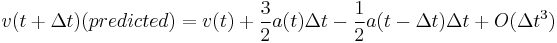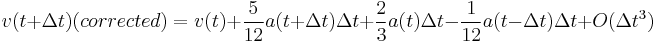Beeman's algorithm

Beeman's algorithm is a method for numerically integrating ordinary differential equations of order 2, more specifically Newton's equations of motion 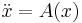$\ddot x=A(x)$ . It was designed to allow high numbers of particles in simulations of molecular dynamics. There is a direct or explicit and an implicit variant of the method. The direct variant was published by Schofield ^[1] in 1973 as personal communication by Beeman. This is what is commonly known as Beeman's method. It is a variant of the Verlet integration method. It produces identical positions, but uses a different formula for the velocities. Beeman^[2] in 1976 published a class of implicit (predictor-corrector) multi-step methods, where Beeman's method is the direct variant of the third order method in this class.

1 Equation
2 Predictor-Corrector Modifications
3 Error term
4 Memory Requirements
5 References

Equation

The formula used to compute the positions at time 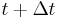$t %2B \Delta t$ in the full predictor-corrector^[2] scheme is:

Predict 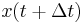$x(t%2B\Delta t)$ from data at times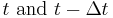 $t\text{ and }t - \Delta t$

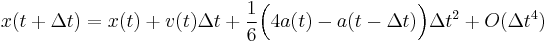$x(t%2B\Delta t) = x(t) %2B v(t) \Delta t %2B \frac{1}{6}\Bigl( 4 a(t) - a(t - \Delta t)\Bigr)\Delta t^2 %2B O( \Delta t^4)$ .

Correct position and velocities at time 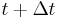$t %2B \Delta t$ from data at times 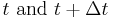$t\text{ and }t%2B\Delta t$ by repeated evaluation of the differential equation to get the acceleration 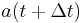$a(t%2B\Delta t)$ and of the equations of the implicit system

$\begin{align} x(t%2B\Delta t) &= x(t) %2B v(t) \Delta t %2B \frac{1}{6}\Bigl(a(t%2B\Delta t) %2B 2a(t)\Bigr)\Delta t^2 %2B O(\Delta t^4);\\ v(t%2B\Delta t)\Delta t &=x(t%2B\Delta t)-x(t) %2B \frac16 \Bigl(2a(t%2B\Delta t) %2B a(t)\Bigr)\Delta t^2 %2B O(\Delta t^4); \end{align}$

In tests it was found that this corrector step needs to be repeated at most twice. The values on the right are the old values of the last iterations, resulting in the new values on the left.

Using only the predictor formula and the corrector for the velocities one obtains a direct or explicit method^[1] which is a variant of the Verlet integration method^[3]:

$\begin{align} x(t%2B\Delta t) &= x(t) %2B v(t) \Delta t %2B \frac{1}{6}\Bigl( 4 a(t) - a(t - \Delta t)\Bigr)\Delta t^2 %2B O( \Delta t^4) \\ v(t%2B\Delta t) &=v(t) %2B \frac16 \Bigl(2a(t%2B\Delta t) %2B 5a(t)-a(t-\Delta t)\Bigr)\Delta t %2B O(\Delta t^3); \end{align}$

</math>. This is the variant that is usually understood as Beeman's method.

Beeman^[2] also proposed to alternatively replace the velocity update in the last equation by the second order Adams–Moulton method:

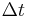$v(t %2B \Delta t) = v(t) %2B \frac{1}{12}\Bigl(5a(t %2B \Delta t) %2B 8a(t) - a(t - \Delta t)\Bigr)\Delta t %2B O(\Delta t^3)$

where

$t$ is present time (i.e.: independent variable)
$\Delta t$ is the time step size
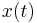$x(t)$ is the position at time t
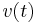$v(t)$ is the velocity at time t
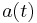$a(t)$ is the acceleration at time t, computed as a function of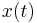 $x(t)$
the last term is the error term, using the big O notation

Predictor-Corrector Modifications

In systems where the forces are a function of velocity in addition to position, the above equations need to be modified into a predictor-corrector form whereby the velocities at time 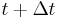$t %2B \Delta t$ are predicted and the forces calculated, before producing a corrected form of the velocities.

An example is:

$x(t%2B\Delta t) = x(t) %2B v(t) \Delta t %2B \frac{2}{3}a(t) \Delta t^2 - \frac{1}{6} a(t - \Delta t) \Delta t^2 %2B O( \Delta t^4).$

The velocities at time t =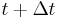 $t %2B \Delta t$ are then calculated from the positions.

$v(t %2B \Delta t) (predicted) = v(t) %2B \frac{3}{2}a(t) \Delta t - \frac{1}{2}a(t - \Delta t) \Delta t %2B O( \Delta t^3)$

The accelerations at time t =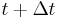 $t %2B \Delta t$ are then calculated from the positions and predicted velocities.

$v(t %2B \Delta t) (corrected) = v(t) %2B \frac{5}{12}a(t %2B \Delta t) \Delta t %2B \frac{2}{3}a(t) \Delta t - \frac{1}{12}a(t - \Delta t) \Delta t %2B O( \Delta t^3)$

Error term

As shown above, the local error term is 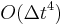$O(\Delta t^4)$ for position and 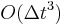$O(\Delta t^3)$ velocity,resulting in a global error of 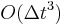$O(\Delta t^3)$ . In comparison, Verlet is 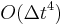$O(\Delta t^4)$ for position and 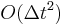$O(\Delta t^2)$ for velocity, however, the more important global error is 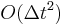$O(\Delta t^2)$ . In exchange for greater accuracy, Beeman's algorithm is moderately computationally more expensive.

Memory Requirements

The simulation must keep track of position, velocity, acceleration and previous acceleration vectors per particle (though some clever work-arounds for storing the previous acceleration vector are possible), keeping its memory requirements on par with velocity Verlet and slightly more expensive than the original Verlet method.

References

^ ^a ^b Schofield, P. (1973), "Computer simulation studies of the liquid state", Computer Physics Communications 5 (1): 17–23, doi:10.1016/0010-4655(73)90004-0
^ ^a ^b ^c Beeman, David (1976), "Some multistep methods for use in molecular dynamics calculations", Journal of Computational Physics 20 (2): 130–139, doi:10.1016/0021-9991(76)90059-0
^ Levitt, Michael; Meirovitch, Hagai; Huber, R. (1983), "Integrating the equations of motion", Journal of Molecular Biology 168 (3): 617–620, doi:10.1016/S0022-2836(83)80305-2, PMID 6193281

Sadus, Richard J. (2002), Molecular Theory of Fluids: Theory, Algorithms and Object-Orientation, Elsevier, p. 231, ISBN 0444510826

Numerical integration

First order methods	Euler method · Backward Euler · Semi-implicit Euler · Exponential Euler

Second order methods	Verlet integration · Velocity Verlet · Crank–Nicolson method · Beeman's algorithm · Midpoint method · Heun's method · Newmark-beta method · Leapfrog integration

Higher order methods	Runge–Kutta methods · List of Runge–Kutta methods · Linear multistep method